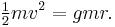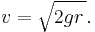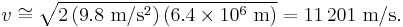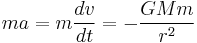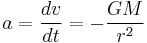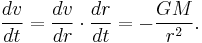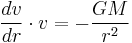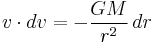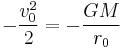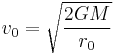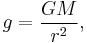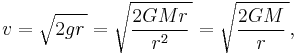Escape velocity
In physics, escape velocity is the speed at which the kinetic energy plus the gravitational potential energy of an object is zero [nb 1]. It is the speed needed to "break free" from a gravitational field without further propulsion.
For a spherically-symmetric body, escape velocity is calculated by the formula
where G is the universal gravitational constant (G=6.67×10-11 m3 kg-1 s-2), M the mass of the planet, star or other body, and r the distance from the centre of gravity.
In this equation atmospheric friction or air drag, is not taken into account. A rocket moving out of a gravity well does not actually need to attain escape velocity to do so, but could achieve the same result at walking speed with a suitable mode of propulsion and sufficient fuel. Escape velocity only applies to ballistic trajectories.
The term escape velocity is actually a misnomer, as the concept refers to a scalar speed which is independent of direction whereas velocity is the measurement of the rate and direction of change in position of an object.
Contents |
Overview
A barycentric velocity is a velocity of one body relative to the center of mass of a system of bodies. A relative velocity is the velocity of one body with respect to another. Relative escape velocities exist only in systems with two bodies. For systems of two bodies the term "escape velocity" is ambiguous, but it is usually intended to mean the barycentric escape velocity of the less massive body. In gravitational fields "escape velocity" refers to the escape velocity of zero mass test particles relative to the barycenter of the masses generating the field.
The phenomenon of escape velocity is a consequence of conservation of energy. For an object with a given total energy, which is moving subject to conservative forces (such as a static gravity field) it is only possible for the object to reach combinations of places and speeds which have that total energy; and places which have a higher potential energy than this cannot be reached at all.
For a given gravitational potential energy at a given position, the escape velocity is the minimum speed an object without propulsion needs, to be able to "escape" from the gravity (i.e. so that gravity will never manage to pull it back). For the sake of simplicity, unless stated otherwise, we will assume that the scenario we are dealing with is that an object is attempting to escape from a uniform spherical planet by moving straight away (along a radial line away from the center of the planet), and that the only significant force acting on the moving object is the planet's gravity.
Escape velocity is actually a speed (not a velocity) because it does not specify a direction: no matter what the direction of travel is, the object can escape the gravitational field (though its path may intersect the planet). The simplest way of deriving the formula for escape velocity is to use conservation of energy. Imagine that a spaceship of mass m is at a distance r from the center of mass of the planet, whose mass is M. Its initial speed is equal to its escape velocity, 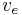 . At its final state, it will be an infinite distance away from the planet, and its speed will be negligibly small and assumed to be 0. Kinetic energy K and gravitational potential energy Ug are the only types of energy that we will deal with, so by the conservation of energy,
. At its final state, it will be an infinite distance away from the planet, and its speed will be negligibly small and assumed to be 0. Kinetic energy K and gravitational potential energy Ug are the only types of energy that we will deal with, so by the conservation of energy,
Kƒ = 0 because final velocity is zero, and Ugƒ = 0 because its final distance is infinity, so
Defined a little more formally, "escape velocity" is the initial speed required to go from an initial point in a gravitational potential field to infinity with a residual velocity of zero, with all speeds and velocities measured with respect to the field. Additionally, the escape velocity at a point in space is equal to the speed that an object would have if it started at rest from an infinite distance and was pulled by gravity to that point. In common usage, the initial point is on the surface of a planet or moon. On the surface of the Earth, the escape velocity is about 11.2 kilometers per second (~6.96 mi/s), which is approximately 34 times the speed of sound (Mach 34) and several times the muzzle velocity of a rifle bullet (up to 1.7 km/s). However, at 9,000 km altitude in "space", it is slightly less than 7.1 km/s.
The escape velocity relative to the surface of a rotating body depends on direction in which the escaping body travels. For example, as the Earth's rotational velocity is 465 m/s at the equator, a rocket launched tangentially from the Earth's equator to the east requires an initial velocity of about 10.735 km/s relative to Earth to escape whereas a rocket launched tangentially from the Earth's equator to the west requires an initial velocity of about 11.665 km/s relative to Earth. The surface velocity decreases with the cosine of the geographic latitude, so space launch facilities are often located as close to the equator as feasible, e.g. the American Cape Canaveral (latitude 28°28' N) and the French Guiana Space Centre (latitude 5°14' N).
The barycentric escape velocity is independent of the mass of the escaping object. It does not matter if the mass is 1 kg or 1,000 kg, what differs is the amount of energy required. For an object of mass  the energy required to escape the Earth's gravitational field is GMm / r, a function of the object's mass (where r is the radius of the Earth, G is the gravitational constant, and M is the mass of the Earth, M=5.9736×1024 kg).
the energy required to escape the Earth's gravitational field is GMm / r, a function of the object's mass (where r is the radius of the Earth, G is the gravitational constant, and M is the mass of the Earth, M=5.9736×1024 kg).
For a mass equal to a Saturn V rocket, the escape velocity relative to the launch pad is 8 nanometers per year faster than the escape velocity relative to the mutual center of mass. When the mass reaches the Andromeda galaxy the earth will have recoiled a third of a mile.
Misconception
Escape velocity is sometimes misunderstood to be the speed a powered vehicle, such as a rocket, must reach to leave orbit and travel through outer space. The quoted escape velocity is commonly the escape velocity at a planet's surface, but it actually decreases with altitude. It is the speed above which an object will depart on a ballistic trajectory, i.e. in free-fall, and never fall back to the surface nor assume a closed orbit. Such an object is said to "escape" the gravity of the planet.
A vehicle with a propulsion system can continue to gain energy and travel away from the planet, in any direction, at a speed lower than escape velocity so long as it is under power. If the vehicle's speed is below its current escape velocity and the propulsion is removed, the vehicle will assume a closed orbit or fall back to the surface. If its speed is at or above the escape velocity and the propulsion is removed, it has enough kinetic energy to "escape" and will neither orbit nor fall back to the surface.
Orbit
If an object attains escape velocity, but is not directed straight away from the planet, then it will follow a curved path. Although this path does not form a closed shape, it is still considered an orbit. Assuming that gravity is the only significant force in the system, this object's speed at any point in the orbit will be equal to the escape velocity at that point (due to the conservation of energy, its total energy must always be 0, which implies that it always has escape velocity; see the derivation above). The shape of the orbit will be a parabola whose focus is located at the center of mass of the planet. An actual escape requires of course that the orbit not intersect the planet nor its atmosphere, since this would cause the object to crash. When moving away from the source, this path is called an escape orbit. Escape orbits are known as C3 = 0 orbits (where C3 = −μ/a, and a is the semi-major axis).
In reality there are many gravitating bodies in space, so that, for instance, a rocket that travels at escape velocity from Earth will not escape to an infinite distance away because it needs an even higher speed to escape the Sun's gravity. In other words, near the Earth, the rocket's orbit will appear parabolic, but eventually its orbit will become an ellipse around the Sun, except when it is perturbed by the Earth whose orbit it must still intersect.
List of escape velocities
| Location | with respect to | Ve[2] | Location | with respect to | Ve[2] | |
|---|---|---|---|---|---|---|
| on the Sun, | the Sun's gravity: | 617.5 km/s | ||||
| on Mercury, | Mercury's gravity: | 4.3 km/s | at Mercury, | the Sun's gravity: | 67.7 km/s | |
| on Venus, | Venus' gravity: | 10.3 km/s | at Venus, | the Sun's gravity: | 49.5 km/s | |
| on Earth, | the Earth's gravity: | 11.2 km/s | at the Earth/Moon, | the Sun's gravity: | 42.1 km/s | |
| on the Moon, | the Moon's gravity: | 2.4 km/s | at the Moon, | the Earth's gravity: | 1.4 km/s | |
| on Mars, | Mars' gravity: | 5.0 km/s | at Mars, | the Sun's gravity: | 34.1 km/s | |
| on Jupiter, | Jupiter's gravity: | 59.5 km/s | at Jupiter, | the Sun's gravity: | 18.5 km/s | |
| on Saturn, | Saturn's gravity: | 35.6 km/s | at Saturn, | the Sun's gravity: | 13.6 km/s | |
| on Uranus, | Uranus' gravity: | 21.2 km/s | at Uranus, | the Sun's gravity: | 9.6 km/s | |
| on Neptune, | Neptune's gravity: | 23.6 km/s | at Neptune, | the Sun's gravity: | 7.7 km/s | |
| on Pluto, | Pluto's gravity: | 1.229 km/s | ||||
| in the solar system, | the Milky Way's gravity: | ≥ 525 km/s [3] | ||||
| on the event horizon, | a black hole's gravity: | = 299,792 km/s |
Because of the atmosphere it is not useful and hardly possible to give an object near the surface of the Earth a speed of 11.2 km/s (40,320 km/h), as these speeds are too far in the hypersonic regime for most practical propulsion systems and would cause most objects to burn up due to atmospheric friction or be torn apart by atmospheric compression. For an actual escape orbit a spacecraft is first placed in low Earth orbit (160–2,000 km) and then accelerated to the escape velocity at that altitude, which is a little less — about 10.9 km/s. The required change in speed, however, is far less because from a low Earth orbit the spacecraft already has a speed of approximately 8 km/s.
Calculating an escape velocity
To expand upon the derivation given in the Overview,
where 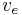 is the barycentric escape velocity, G is the gravitational constant, M is the mass of the body being escaped from, r is the distance between the center of the body and the point at which escape velocity is being calculated, g is the gravitational acceleration at that distance, and μ is the standard gravitational parameter.[4]
is the barycentric escape velocity, G is the gravitational constant, M is the mass of the body being escaped from, r is the distance between the center of the body and the point at which escape velocity is being calculated, g is the gravitational acceleration at that distance, and μ is the standard gravitational parameter.[4]
The escape velocity at a given height is 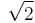 times the speed in a circular orbit at the same height, (compare this with equation (14) in circular motion). This corresponds to the fact that the potential energy with respect to infinity of an object in such an orbit is minus two times its kinetic energy, while to escape the sum of potential and kinetic energy needs to be at least zero. The velocity corresponding to the circular orbit is sometimes called the first cosmic velocity, whereas in this context the escape velocity is referred to as the second cosmic velocity"[5]
times the speed in a circular orbit at the same height, (compare this with equation (14) in circular motion). This corresponds to the fact that the potential energy with respect to infinity of an object in such an orbit is minus two times its kinetic energy, while to escape the sum of potential and kinetic energy needs to be at least zero. The velocity corresponding to the circular orbit is sometimes called the first cosmic velocity, whereas in this context the escape velocity is referred to as the second cosmic velocity"[5]
For a body with a spherically-symmetric distribution of mass, the barycentric escape velocity 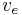 from the surface (in m/s) is approximately 2.364×10−5 m1.5kg−0.5s−1 times the radius r (in meters) times the square root of the average density ρ (in kg/m³), or:
from the surface (in m/s) is approximately 2.364×10−5 m1.5kg−0.5s−1 times the radius r (in meters) times the square root of the average density ρ (in kg/m³), or:
Deriving escape velocity using calculus
These derivations use calculus, Newton's laws of motion and Newton's law of universal gravitation.
Derivation using only g and r
the Earth's escape speed can be derived from "g," the barycentric acceleration due to gravity at the Earth's surface. It is not necessary to know the gravitational constant G or the mass M of the Earth. Let
- r = the Earth's radius, and
- g = the barycentric acceleration of gravity at the Earth's surface.
Above the Earth's surface, the acceleration of gravity is governed by Newton's inverse-square law of universal gravitation. Accordingly, the acceleration of gravity at height s above the center of the Earth (where s > r ) is g (r / s)2. The weight of an object of mass m at the surface is g m, and its weight at height s above the center of the Earth is gm (r / s)2. Consequently the energy needed to lift an object of mass m from height s above the Earth's center to height s + ds (where ds is an infinitesimal increment of s) is gm (r / s)2 ds. Since this decreases sufficiently fast as s increases, the total energy needed to lift the object to infinite height does not diverge to infinity, but converges to a finite amount. That amount is the integral of the expression above:
That is how much kinetic energy the object of mass m needs in order to escape. The kinetic energy of an object of mass m moving at speed v is (1/2)mv2. Thus we need
The factor m cancels out, and solving for v we get
If we take the radius of the Earth to be r = 6400 kilometers and the acceleration of gravity at the surface to be g = 9.8 m/s2, we get
This is just a bit over 11 kilometers per second, or a bit under 7 miles per second, as Isaac Newton calculated.
Derivation using G and M
Let G be the gravitational constant and let M be the mass of the earth and 'm' be the mass of other body to be escaped.
By applying the chain rule, we get:
Because 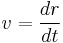
Since we want escape velocity
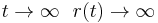 and
and 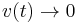
v0 is the escape velocity and r0 is the radius of the planet. Note that the above derivation relies on the equivalence of inertial mass and gravitational mass.
Consistency of derivations
The barycentric gravitational acceleration can be obtained from the gravitational constant G and the mass of Earth M:
where r is the radius of Earth. Thus
so the two derivations given above are consistent.
Multiple sources
The escape velocity from a position in a field with multiple sources at rest with respect to each other is derived from the total potential energy per kg at that position, relative to infinity. The potential energies for all sources can simply be added. For the escape velocity it can be shown that this gives an escape velocity which is equal to the square root of the sum of the squares of the individual escape velocities due to each source.
For example, at the Earth's surface the escape velocity for the combination Earth and Sun would be 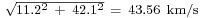 .
.
See also
- Orbital speed
- Characteristic energy (C3)
- Delta-v budget – speed needed to perform manoeuvres.
- Gravitational slingshot – a technique for changing trajectory.
- Gravity well
- Two-body problem
- Black hole – an object with an escape velocity greater than the speed of light
- Oberth effect – burning fuel deep in a gravity field gives higher change in velocity.
- Newton's cannonball
- List of artificial objects escaping from the Solar System
- List of artificial objects in heliocentric orbit
Notes
- ^ gravitational potential energy is negative since gravity is an attractive force and the potential is defined to be zero at infinity
References
- Roger R. Bate, Donald D. Mueller, and Jerry E. White (1971). Fundamentals of astrodynamics. New York: Dover Publications. ISBN 0-486-60061-0.
- ^ http://nssdc.gsfc.nasa.gov/nmc/spacecraftDisplay.do?id=1959-012A
- ^ a b "Solar System Data". Georgia State University. http://hyperphysics.phy-astr.gsu.edu/hbase/solar/soldata2.html. Retrieved 2007-01-21.
- ^ [1]
- ^ Bate, Mueller and White, p. 35
- ^ Teodorescu, P. P. (2007). Mechanical systems, classical models. Springer, Japan. p. 580. ISBN 1-402-05441-6. http://books.google.com/books?id=k4H2AjWh9qQC&pg=PA580., Section 2.2.2, p. 580
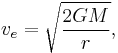
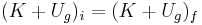
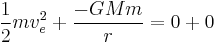
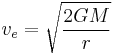
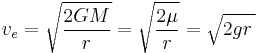
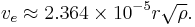
![\begin{align}
\int_r^\infty gm \left(\frac{r}{s}\right)^2 \, ds
& = gmr^2 \int_r^\infty s^{-2}\,ds
= gmr^2 \left[-s^{-1}\right]_{s:=r}^{s:=\infty} \\
& = gmr^2\left(0-(-r^{-1})\right)=gmr.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/45a05fc05991c8dd772c24310d8d7a86.png)